Einleitung
In diesem Blogbeitrag soll es um eine sehr interessante Herausforderung gehen, auf die ich im Rahmen der Ausbildung unserer Werkstudenten traf. Immerhin konnte ich sie bisher mit den Standard-T-SQL-Mitteln nicht lösen. Das faszinierende Element an der Aufgabe ist die Einfachheit der Fragestellung bei extrem übersichtlicher Datenmenge sowie der einfache Aufbau der Testdaten. Konnte es wirklich sein, dass mich eine simple Tabelle mit nur zwei Spalten und nur 12 Datensätzen derart ins Schwitzen bringt, wo ich doch auf über 15 Jahren Erfahrungen mit dem SQL Server von Microsoft zurückblicken kann und fast täglich damit programmiere? Somit entstand die Idee für das Teilsummenproblem im SQL Server.
Anregung zur Idee
Für meinen Konferenz-Vortrag „richtig harte Kopfnüsse mit T-SQL.“ habe ich zuerst überlegt, wo mir dieses theoretische Konstrukt, welches in der Mathematik und Informatik als „Teilsummenproblem“ bekannt ist, schon mal im Alltag über den Weg gelaufen ist. Letztendlich kennen alle das Lehrbuchbeispiel eines Bankräubers, der nur auf eine begrenze Rucksackkapazität zum Abtransport der Beute zugreifen kann und nun entscheiden muss, welche Säcke er einpackt und welche er aus Platz- und Gewichtsgründen zurücklassen muss. Schließlich fiel mir eine Anfrage meines kleinen Sohnes ein. Mit Colin hatten wir in jungen Jahren folgende Vereinbarung bei dem Besuch eines Kirmesplatzes getroffen:
- Colin muss kein eigenes Taschengeld investieren, denn er bekommt genauso wie seine größere Schwester eine individuelle Summe von Oma, Opa und den Eltern zur Verfügung gestellt.
- Anfangs darf er sich im Internet informieren, welche Fahrgeschäfte der Rummel bietet und welche Möglichkeiten der Verköstigung er gerne aufsuchen möchte.
- Nachdem die Freigabe der jeweiligen Attraktion erfolgt, darf er eine Liste anfertigen, wie er die zur Verfügung stehende Summe ausgeben möchte. Dabei gibt es keine Einschränkungen. Theoretisch könnte er alles in Eis oder Geisterbahnfahrten investieren. Des Weiteren kann er die Attraktionen aber auch beliebig kombinieren.
- Colin ist von dem Typ Kinder, die gerne am nächsten Schultag bei allen Themen mitredet. Daher versucht er so viele verschiedene Attraktionen wie möglich zu nutzen
- Letztendlich führt seine Sparsamkeit dazu, dass er
- … keinesfalls das gesetzte Limit überschreiten wird, schließlich müsste er sonst eigenes Taschengeld opfern
- … den zur Verfügung gestellten Betrag so weit wie nur eben möglich ausreizt, somit würde kein Geld verschwendet werden, denn
ungenutzte Beträge verfallen und gehen zurück an Oma, Opa und die Eltern!
Die Hilfe naht
Somit war Colin mit dieser kleinen und vermutlich so simplen Matheaufgabe tagelang in seinem Zimmer verschwunden und optimierte mit Papier und Bleistift vor sich hin. Für einen Grundschüler war seine Rechenleistung auf jeden Fall enorm. Ungeachtet des Blog-Beitrags: alleine für diese extra Lerneinheit ist das Verfahren zu empfehlen ? Irgendwann kam er in Begleitung seiner großem Schwester Neela in mein Zimmer und forderte mich auf, das Problem für die Zukunft mit Rechnerunterstützung zu lösen – schließlich sei ich ja Informatiker. Also warf ich den SQL Server an und schaffte erstmal die Grundvoraussetzungen: Eine entsprechende Tabelle mit Testdaten.
Die Grundlagen schaffen
— Schema OKTOBERFEST anlegen, sodass Objekte sauber der Aufgabe zugeordnet werden können
CREATE SCHEMA [Oktoberfest]
GO
— Des Weiteren Tabelle ATTRAKTION im Schema OKTOBERFEST anlegen
CREATE TABLE [Oktoberfest].[Attraktion](
[ID] [INT] PRIMARY KEY IDENTITY(1,1), [Attraktion] [NVARCHAR](20) NULL
, [Preis] [MONEY] NULL
) ON [PRIMARY]
GO
— Dann Tabelle ATTRAKTION im Schema OKTOBERFEST mit den Inhalten (beispielhafte Testdaten) aus der Fragestellung füllen
INSERT INTO [Oktoberfest].[Attraktion] VALUES
(‚Kettenkarussell‘, 2.15)
, (‚Geisterbahn‘, 4.50)
, (‚Raupe‘, 2.80)
, (‚Würstchenstand‘, 4.20)
, (‚Softgetränk‘, 1.75)
, (‚Riesenrad‘, 5.30)
, (‚Autoscooter‘, 3.10)
, (‚Entenangeln‘, 2.40)
, (‚Dosenwerfen‘, 2.05)
, (‚Losbude‘, 1.55)
, (‚Wilde Maus‘, 4.30)
, (‚Kamelrennen‘, 1.60)
Das berühmte Urnenmodell
Doch wie sollte man nun die gewünschten Informationen extrahieren? Trotz des simplen Aufbaus und der geringen Zahl der Testdaten schlug die gewaltige Komplexitätskeule der Kombinatorik gnadenlos zu. Schließlich wurde mir klar: betrachtet man die Fragestellung mit etwas Mathematik, entspricht die Herausforderung nach etwas Vereinfachung (bspw. der Anpassung des Einzelpreises je Attraktion auf einen Durchschnitt) der des berühmten „Urnenmodells mit Zurücklegen“.
/*
Wir nennen die Zahl der Kugeln im folgenden (=Attraktionen) „n“ und die Anzahl der Ziehungen (Fahrten/Einkäufe)
„k“. Die Reihenfolge, in der die Kugeln gezogen werden, ist irrelevant.
Es gilt die mathematische Formel aus der Kombinatorik:
n + k – 1
Anzahl Möglichkeiten = ( )
n – 1
_________________________________________________________________________________________________________________
Bei einem Durchschnittspreis von bspw. 3 Euro pro Attraktion und einem Budget von 21 Euro kann man 7 Einkäufe
tätigen. Werden weiterhin, wie im Beispiel, 12 Attraktionen angeboten, ergibt dies:
12 + 7 – 1 18 18! 18!
Anzahl Möglichkeiten = ( ) = ( ) = ————– = ——–
12 – 1 11 (18-11)! * 11! 7! * 11!
6.402.373.705.728.000 6.402.373.705.728.000
= ———————- = ——————— ~ 31.835
5.040 * 39.916.800 201.180.672.000
_________________________________________________________________________________________________________________
Bei einem Durchschnittspreis 2,50 Euro, einer Auswahl aus 20 Attraktionen und einem Budget von 30 Euro erreicht die Anzahl der Kombinationen schließlich Höhen, die die TempDB vor ernsthafte Probleme stellen kann:
20 + 12 – 1 31 31! 31!
Anzahl Möglichkeiten = ( ) = ( ) = ————– = ——–
20 – 1 19 (31-19)! * 19! 12! * 19!
8.22283865418E+33 8.22283865418E+33
= ————————————- = ——————— ~ 141.120.525
479.001.600 * 121.645.100.408.832.000 5,826819772799118e+23
*/
Kreieren der Prozedur
Somit war relativ schnell klar, dass manuell erstellte Schleifen und Cursor hier nicht zielführend nutzbar sind. Denn derartige Ideen lassen sich einfach nicht effizient umsetzen und bedeuten dann in der Laufzeitbetrachtung die Rote Karte. Aber der SQL Server kennt ja noch ein paar mehr Wege. Denn ich kam mit einer rekursiven CTE relativ schnell zum Ziel. Schließlich ist diese einfach zu verstehen und zu warten. Außerdem ist sie schon durch Microsoft laufzeitoptimiert und einfach aufzurufen. Um das ganze praktisch zu gestalten, habe ich die CTE in eine Stored Procedure ausgelagert:
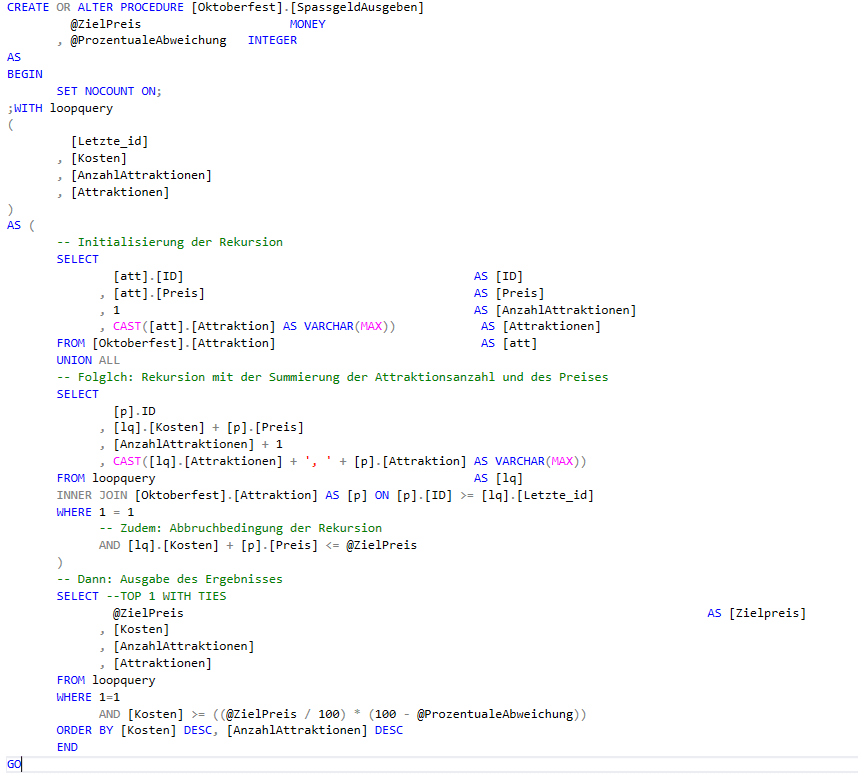
— ### Hinweis: ###
— Kurzum: Ein-/Auskommentiertes „TOP 1 WITH TIES“ beeinflusst, wie viele und ob gleichwertige, bestplatzierte oder nur genau eine bestimmte Anzahl bestplatzierter Lösungen angezeigt werden sollen
Aufruf der Prozedur
Der Aufruf der CTE-Prozedur geht schließlich schnell von der Hand. Man bestückt die notwendigen Parameter und übergibt der Prozedur somit die Information, wie hoch die zur Verfügung stehende Summe ist und ob diese genau zu treffen ist. Außerdem muss man angeben ob eine Abweichung nach oben oder unten zu tolerieren ist. Dieser Schwellwert ist in Prozent anzugeben.
SET STATISTICS XML ON
DECLARE @RC INTEGER
DECLARE @ZielPreis MONEY
DECLARE @ProzentualeAbweichung INTEGER
SET @ZielPreis = 8.05
SET @ProzentualeAbweichung = 0
EXECUTE @RC = [Oktoberfest].[SpassgeldAusgeben]
@ZielPreis, @ProzentualeAbweichung
GO
SET STATISTICS XML OFF
GO
Übergibt man der Prozedur mit 21.80 Euro sowie einer erlaubten Abweichung von 2% andere Parameter, ermittelt der SQL Server schon 16.030 mögliche Kombinationen, die die gestellten Bedingungen erfüllen. Dabei wird das Ergebnis nach Grad der Erreichung der Vorgabesumme sowie nach Anzahl der damit nutzbaren Attraktionen sortiert:
DECLARE @RC INTEGER
DECLARE @ZielPreis MONEY
DECLARE @ProzentualeAbweichung INTEGER
SET @ZielPreis = 21.80
SET @ProzentualeAbweichung = 2
EXECUTE @RC = [Oktoberfest].[SpassgeldAusgeben]
@ZielPreis, @ProzentualeAbweichung
GO
Infolgedessen stand nun auf dem Plan, eine Lösung zu entwickeln, die die Anzahl der unterschiedlichen Attraktionen zählt. Danach zu sortieren ist dann nur noch eine Fingerübung…






